Come è noto, il rapporto tra la circonferenza di un cerchio ed il suo diametro determina la costante matematica pi greco (π =3,1459…); meno nota è la costante chiamata φ (phi=1,6180339887…), meglio conosciuta come sezione aurea, che ha in comune con π il fatto di essere un numero irrazionale, ovvero avente una parte decimale infinita e non periodica.
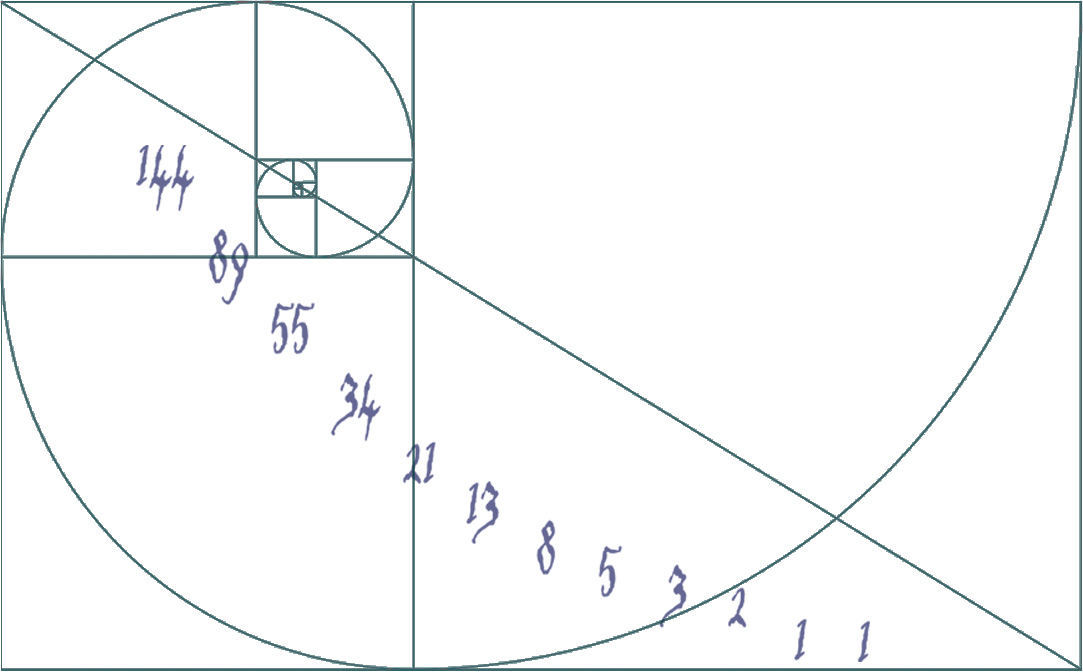
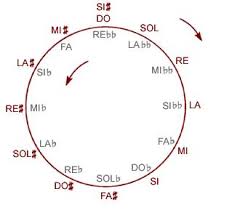 Ora Facciamo una piccola premessa che ci tornerà utile in seguito. Tutti quelli che hanno fatto degli studi musicali hanno sicuramente familiarità con il circolo delle quinte, quindi tralascio oltre ulteriore spiegazione a riguardo. Molti sapranno anche che esso rappresenta un espediente del sistema a temperamento equabile usato in occidente da un certo periodo in poi che permette, tramite opportuni calcoli e conseguenti accordature di dividere l’ottava in 12 semitoni equidistanti fra di loro; ma se consideriamo gli armonici naturali prodotti da una corda vibrante ( vale per qualsiasi altra tipologia di generazione acustica) , il circolo delle quinte non si chiude affatto ma diventa una spirale come quella della figura in alto. Ovvero, nella scala pitagorica il circolo delle quinte dopo dodici suoni non si chiude sulla nota di partenza un ottava sopra : l’intervallo residuo è detto comma pitagorico che varia da ottava in ottava in modo infinito e decrescente. Questo in teoria perchè in pratica la fisiologia del nostro sistema uditivo non ci permette di discernere intervalli piccoli oltre un certo limite, ne tanto meno l’ascolto di frequenze oltre una determinata altezza. Finita la premessa.
Ora Facciamo una piccola premessa che ci tornerà utile in seguito. Tutti quelli che hanno fatto degli studi musicali hanno sicuramente familiarità con il circolo delle quinte, quindi tralascio oltre ulteriore spiegazione a riguardo. Molti sapranno anche che esso rappresenta un espediente del sistema a temperamento equabile usato in occidente da un certo periodo in poi che permette, tramite opportuni calcoli e conseguenti accordature di dividere l’ottava in 12 semitoni equidistanti fra di loro; ma se consideriamo gli armonici naturali prodotti da una corda vibrante ( vale per qualsiasi altra tipologia di generazione acustica) , il circolo delle quinte non si chiude affatto ma diventa una spirale come quella della figura in alto. Ovvero, nella scala pitagorica il circolo delle quinte dopo dodici suoni non si chiude sulla nota di partenza un ottava sopra : l’intervallo residuo è detto comma pitagorico che varia da ottava in ottava in modo infinito e decrescente. Questo in teoria perchè in pratica la fisiologia del nostro sistema uditivo non ci permette di discernere intervalli piccoli oltre un certo limite, ne tanto meno l’ascolto di frequenze oltre una determinata altezza. Finita la premessa.
L’esempio più semplice di rappresentazione della sezione aurea è quello di una retta :
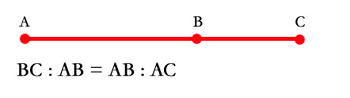
Dove il segmento BC sta al segmento AB come AB sta all’intera retta AC.
Il numero aureo può anche essere espresso con una certa approssimazione (essendo un numero irrazionale non può essere quantificato esattamente con una frazione) dal numero 8/5 ; 13/8; 21/13 e via dicendo in altre molteplici combinazioni.
Vediamo ora una figura geometrica come il rettangolo aureo; La storia si fa più interessante: 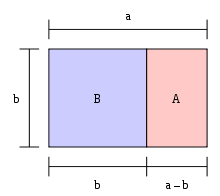 Se applicassimo ulteriolmente la sezione aurea anche al rettangolo A e continuassimo in modo analogo, otterremmo quello che si vede nella figura in basso.
Se applicassimo ulteriolmente la sezione aurea anche al rettangolo A e continuassimo in modo analogo, otterremmo quello che si vede nella figura in basso. 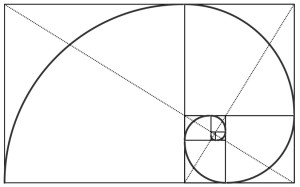 Dove la curva che unisce la suddivisione dei rettangoli aurei è una spirale logaritmica.Ora ci torna utile quanto esposto nella premessa dove avevamo accennato che il circolo delle quinte, se consideriamo i suoni armonici naturali, si trasforma in una spirale. Se supponiamo il primo quadrilatero aureo (quello grande) rappresenti l’insieme delle 12 note della scala pitagorica di partenza, la successiva divisione sarà l’insieme delle 12 note leggermente diverse dalle prime in virtù del comma pitagorico, e così di seguito a scendere fino teoricamente all’infinito. Se osservassimo con un microscopio all’interno del rettangolo più piccolo troveremmo sempre la stessa figura di partenza. Da un punto di vista morfologico la figura rappresenta un frattale.
Dove la curva che unisce la suddivisione dei rettangoli aurei è una spirale logaritmica.Ora ci torna utile quanto esposto nella premessa dove avevamo accennato che il circolo delle quinte, se consideriamo i suoni armonici naturali, si trasforma in una spirale. Se supponiamo il primo quadrilatero aureo (quello grande) rappresenti l’insieme delle 12 note della scala pitagorica di partenza, la successiva divisione sarà l’insieme delle 12 note leggermente diverse dalle prime in virtù del comma pitagorico, e così di seguito a scendere fino teoricamente all’infinito. Se osservassimo con un microscopio all’interno del rettangolo più piccolo troveremmo sempre la stessa figura di partenza. Da un punto di vista morfologico la figura rappresenta un frattale.
Possiamo quindi concludere che l’acustica, nella relazione numerica che intercorre tra gli armonici naturali nelle differenti ottave ha di per se una relazione aurea, a prescindere da ogni forma strutturale compositiva finalizzata ad essa. La sezione aurea si trova anche sorprendentemente nella biologia, nella fisica, nella pittura, nell’ architettura, nella scultura, nella fotografia e persino nella poesia. Tanto da farla associare fin dalle epoche più remote ad mito di canone estetico di bellezza assoluto o di proporzione divina attribuendogli spesso un falso significato mistico-esoterico.
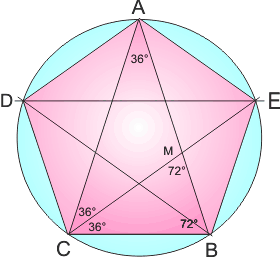
il rapporto tra il lato CB e la digonale AB è 0,6180…ovvero il numero Aureo
Gli antichi greci conoscevano bene la sezione aurea; non vi è dubbio che essa fu usata consciamente da alcuni architetti e scultori greci, particolarmente nella struttura del partenone. Il matematico Mark Barr pensava a questo quando nel 1918 dette al rapporto il simbolo di φ. Essa è la prima lettera greca nel nome del grande Fidia che si ritiene abbia usato con frequenza il rapporto aureo nelle sue sculture. Forse una ragione per cui la comunità pitagorica scelse il pentagramma o la stella a cinque punte come simbolo del suo ordine dipende dal fatto che se uniamo i suoi vertici, otteniamo un pentagono regolare il quale ha la diagonale ed un lato esattamente in rapporto aureo. Dobbiamo giungere al medioevo per trovare un esplicito riferimento scritto che menzioni il rapporto aureo, visto che i greci ed i pitagorici in particolare si tenevano ben stretto questo segreto che non doveva essere rivelato a nessuno. Gianblico nel IV secolo d.C. narra del filosofo pitagorico Ippaso da Metaponto, morto in mare come empio perchè ritenuto colpevole dagli Dei per aver rivelato la dottrina degli irrazionali e degli incommensurabili e sul segreto della costruzione della sfera di dodici pentagoni, ovvero del dodecaedro, uno dei cinque solidi platonici. Il matematico Fibonacci XII secolo, nel suo libro “Liber Abaci” espone i fondamenti di algebra e matematica usati nei paesi arabi. Un problema che il matematico si pose fornisce l’occasione per l’introduzione della serie di Fibonacci che si riscontra in numerosi esempi in natura, ed ha uno strettissimo legame di parentela con il Numero Aureo.
Un contadino chiuse nella sua conigliera una coppia di conigli per avviare un allevamento. La coppia prese a prolificare il secondo mese una nuova coppia di conigli. Nei mesi che seguirono la coppia capostipite continuò a generare regolarmente una coppia al mese, e altrettanto fece ciascuna delle coppie generate, ciascuna però a partire dal secondo mese dopo la propria nascita. Quante coppie di conigli popolarono la conigliera dopo il decimo mese se nel frattempo non morì nessun coniglio?
La soluzione fu questa serie numerica dove il numero che segue è il risultato della somma dei due numeri che lo precedono.
1 ; 1 ; 2 ; 3 ; 5 ; 8 ; 13 ; 21 ; 34 ; 55 ; 89 ; 144 ; 233 ; 377 ; …
La correlazione con la sezione aurea è data dal fatto che, escludendo i primi tre numeri, se prendiamo qualsiasi numero e lo dividiamo con quello che lo precede avremmo come risultato il numero aureo φ 1,6180339887… con un approssimazione sempre più precisa in funzione della grandezza dei numeri scelti.
Ad esempio se prendiamo numeri 8 e 5 avremmo 8/5 = 1,6. Mentre se consideriamo 377/233 =1,6180257510… con un grado di precisione sempre maggiore con numeri più grandi.
Considerare la serie di Fibonacci per comporre musica rappresenta un modo semplice ed efficace per applicare rigorosamente con raziocinio la sezione aurea. Possiamo analizzare almeno quattro metodologie fondamentali di strutture compositive formali a sezione aurea:
L’armonia aurea diatonica è la forma più semplice e facilmente individuabile all’interno di una partitura. Ecco un semplice esempio che utilizza la serie di Fibonacci per la costruzione di accordi basati sul rapporto aureo:

Come si può notare questa cadenza è costruita su sei numeri della serie di Fibonacci discendenti e trasportati di ottava i secondi tre. Corrisponde a quella che viene definita in armonia, non a caso, cadenza perfetta.
Nulla vieta di costruire accordi a quattro o più voci, oppure scegliere un’altra sequenza di numeri della serie. Le possibilità sono molteplici e spesso i risultati estetici sono sorprendenti.
Considerando il ritmo
Dopo l’armonia possiamo considerare il ritmo per il nostro fine, inteso sia come velocità relativa metronomica che assoluta, decidendo a priori la durata del brano espressa in minuti- secondi. Ecco un esempio:
Supponiamo di avere un brano di 89 battute nella forma A B A1 e vogliamo dividerlo in modo aureo, avremo la sezione: A fino alla battuta 21, la B fino alla 34 e la A1 fino alla battuta 89.
Il discorso si fa leggermente più complesso se il nostro brano presenta al suo interno delle variazioni metronomiche, allora non potremmo più applicare il procedimento di cui sopra in quanto la divisione aurea applicata alle battute sarebbe completamente errata da un punto di vista matematico. Si può ovviare a questo considerando come riferimento la durata del brano secondo la codifica cronologica con l’unico problema che la variazione tematica avverrebbe all’interno di una battuta e non all’inizio. Nulla vieta l’uso di contemporaneo annidato di diverse strutture formali a sezione aurea, con gradi di complessità sempre maggiore e di difficile individuazione per l’ascoltatore.
Un trattato del 1509 del matematico Luca Pacioli, intitolato De Divina Proportione ed illustrato da Leonardo da Vinci è un affascinante compendio delle apparizioni di Φ in varie figure piane e solide nel rinascimento.La sezione aurea suscitò grande interesse tra artisti e matematici del rinascimento, tra cui: Leon Battista Alberti (1404-1472) Piero della Francesca (1416-1492) e Botticelli (1445-1510) .

Alcuni esempi di sezione aurea in natura



A diversi compositori viene attribuito di usare la SA nei propri lavori, senza che essi abbiano lasciato scritto in partitura riferimenti precisi sull’uso della SA. Molto spesso si fanno delle congetture che non hanno molto senso a riguardo, visto che i numeri possono essere manipolati in vari modi anche in buona fede, e non di rado lo studioso fa coincidere con degli artifici le sue aspettative sulle conclusioni finali nell’analisi della partitura. Il terreno è molto scivoloso se non si esegue un’indagine rigorosa compatibile con il metodo scientifico. Inoltre, le tracce potrebbero essere, come abbiamo visto, annidate e quindi quasi impossibili da trovare.
Molto spesso capita che nelle opere pittoriche di diversi artisti venga riscontrata la presenza della sezione aurea, in particolar modo sotto forma di rettangolo aureo, e molto spesso a sproposito; anche diversi siti internet, nonché libri, caldeggiano ferventemente questa ipotesi, a volte azzardata, col rischio di consolidare l’esistenza di un falso mito: ovvero, la presunta superiorità estetica della sezione aurea. Occorre invece muoversi con cautela, pure in questo ambito perché la presunta presenza della sezione può in molte opere essere frutto di plurimi fattori, che possono trarre in inganno e indurre a facili considerazioni affrettate; tre paiono essere i più importanti:
- Tralasciando le ovvie possibilità di imprecisioni nelle misurazioni, a volte viene affermata la presenza del rapporto aureo pur trovandosi di fronte a numeri quali
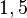 ,
,  ,
,  e
e  frettolosamente assimilati a sue “buone” approssimazioni. Nonostante l’evidente difficoltà di approssimazione di un numero irrazionale con la dovuta precisione, bisogna almeno considerare l’eventualità che l’artista abbia voluto sì usare misure non arbitrarie, ma, forse, semplicemente rifacendosi a rapporti fra numeri interi; così com’è possibile d’altronde che abbia volutamente usato numeri vicini al rapporto aureo proprio per tentare di approssimarlo.
frettolosamente assimilati a sue “buone” approssimazioni. Nonostante l’evidente difficoltà di approssimazione di un numero irrazionale con la dovuta precisione, bisogna almeno considerare l’eventualità che l’artista abbia voluto sì usare misure non arbitrarie, ma, forse, semplicemente rifacendosi a rapporti fra numeri interi; così com’è possibile d’altronde che abbia volutamente usato numeri vicini al rapporto aureo proprio per tentare di approssimarlo. - Le misurazioni spesso sono state effettuate prendendo a riferimento punti arbitrari o sulla cui oggettività è tuttora aperto un dibattito; inoltre non è da escludere, la non poi tanto remota possibilità che in un sistema complesso, formato da diversi elementi, rapporti prossimi al valore aureo possano formarsi per fattori ascrivibili al caso, pure in mancanza di un’effettiva volontà dell’artista.
- Il convincimento della sua superiorità estetica e la riproposizione di modelli familiari, se non canonici, possono aver indotto l’artista a copiare o a ispirarsi da forme e proporzioni di opere di altri artisti dove la sezione aurea era effettivamente o approssimativamente presente, e quindi averla involontariamente riprodotta nella propria opera.
A fronte di queste considerazioni, si può capire come sia pienamente lecito affermare la presenza della sezione aurea, in un’opera o nell’estetica di un artista, soltanto in presenza di forti indizi che indicano che l’artista ha volutamente e consciamente utilizzato tale sezione nelle sue opere, o per sua ammissione diretta.
Sul piano compositivo la sezione aurea attraverso la serie di Fibonacci può, ovviamente, essere rapportata a qualsiasi unità di misura concernente la musica, cioè durata temporale di un brano, numero di note o di battute, ecc. non sono comunque rari anche in questo caso facili entusiasmi dovuti a fraintendimenti numerici. Per esempio Paul Larson nel 1978 sostenne di aver riscontrato nei Kyrie contenuti nel Liber Usualis, il rapporto aureo a livello delle proporzioni melodiche, ma in mancanza di una documentazione che ne attesta la volontà di inserimento rimane tutto a livello puramente congetturale.
Béla Bartók (1881-1945) in alcune delle sue maggiori composizioni (come la Musica per Archi, Percussioni e Celesta) e Claude Debussy (1862-1918), il quale era particolarmente attratto dalla sezione aurea, citata da lui come le divin nombre nella raccolta Estampes (1903) e usata, tra gli altri, nella composizione dei brani La Mer (1905) e Cathédrale Engloutie.
Quest’ultimo, in particolare, è un preludio per pianoforte di 89 battute, di cui le prime 68 hanno un tempo doppio delle restanti 21: in altre parole, alla battuta 68 il brano rallenta e la durata delle note si dimezza. L’effetto prodotto all’ascolto, quindi, riduce le battute di questa prima sezione a 34, e il brano ha una lunghezza percepita da chi lo ascolta di 55 battute, vale a dire la sezione aurea di 89. Questo è uno dei tanti esempi che si possono citare per descrivere l’applicazione del concetto di sezione aurea all’interno delle composizioni musicali di Debussy. Il pianista Roy Howat ha analizzato altri brani di Debussy come Reflets dans l’eau, L’isle joyeuse (oltre al già citato La Mer) riscontrando in ognuno varie applicazioni delle tecniche succitate.
Bartók e Debussy sono solo due tra i compositori che hanno usato in musica il concetto di sezione aurea, ma se ne potrebbero menzionare molti altri, tutti operanti tra la fine delXIX secolo e il XX secolo. In epoche più recenti, musicisti quali Stockhausen, Pierre Barbaud, Iannis Xenakis, facendo evolvere i precedenti utilizzi della matematica in musica, hanno introdotto un utilizzo più strutturato della matematica (soprattutto il calcolo delle probabilità e del computer per la composizione musicale).
