I rapporti che legano la musica e la matematica sono noti da moltissimo tempo, si consideri gli studi  della  scuola pitagorica intorno al 450 a.c. sulle corde vibranti, dove si scoprì che dividendo una corda in due parti uguali si otteneva lo stesso suono ma di altezza superiore (ottava) rispetto alla corda intera.

Pitagora avrebbe quindi tradotto sperimentalmente la sua intuizione costruendo un monocordo. Egli tese una corda fra due ponticelli e ricavò l’ottava ponendo una stanghetta esattamente al centro della corda (1:2). Poi ne pose un’altra a 2/3 della lunghezza della corda, stabilendo così l’intervallo di 5a. Sistemando a 3/4 un’altra stanghetta trovò così l’intervallo di 4a. La distanza, in termini di altezza, fra la 4a e la 5a fu per lui molto importante e la chiamò tono.

Dobbiamo probabilmente a lui il concetto di divisione dell’ottava. La scala musicale basata su questi intervalli, che nel Medioevo era attribuita correntemente allo stesso Pitagora, ebbe una particolare importanza teorica, al di là della pratica musicale: Platone, nel dialogo Timeo, la descrisse come fondamento numerico dell’anima del mondo. Nel corso del Medioevo, sulla base del racconto della scoperta delle proporzioni numeriche corrispondenti agli intervalli musicali, riportato da Boezio e da Proclo, Pitagora fu considerato l’inventore della teoria musicale (cit.wikipedia).

Fatta questa breve ed incompleta premessa, con l’unico scopo di accennare l’intima corrispondenza tra musica e matematica ( in altri capitoli del blog nella sezione acustica vi è una trattazione più approfondita di questo argomento), passiamo ora alla ragione di essere di questo articolo: ovvero l’idea  di inserire la partitura in un sistema cartesiano  e ricondurre tutte le informazioni contenute in essa in una serie numerica che fosse facilmente suonabile a prima vista. Partiamo dal presupposto che quanto descriverò i non ha minimamente la pretesa di essere alternativo al sistema di notazione tradizionale usato da molti secoli a questa parte, ne tanto meno di esserne solo anche parzialmente sostitutivo.

Analizziamo due battute di un semplice spartito scritto nel modo tradizionale

 

 

 

 

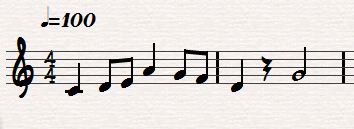
Ora inseriamo il nostro spartito in un sistema cartesiano

 

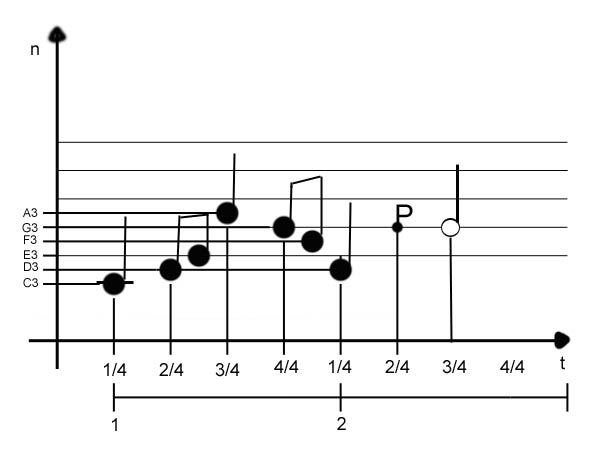
Dove avremo sull’asse delle ascisse il tempo (t) , mentre sull’asse delle ordinate  la rappresentazione delle note reali (n).

Il passo successivo sarà quello di scrivere le nostre due battute come sequenza numerica:

Ora per completezza aggiungiamo anche il tempo , la velocità metronomica e l’inizio e la fine del brano.

Possiamo osservare che ogni battuta è compresa nelle parentesi tonde; le parentesi graffe rappresentano gli identificatori del ritmo e del movimento .

Analizziamo un altro esempio

 

Trascrivendolo in forma numerica diventa

 

 

 

 

 

 

 

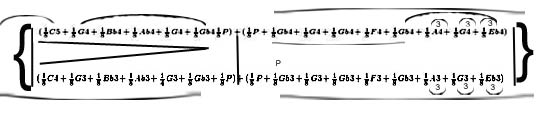
Vediamo ora un altro esempio con la notazione armonica:

 

 

 

 

Avremo:

 

 

 

 

 

 

 

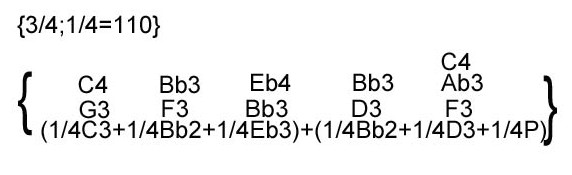
Possiamo notare che basta aggiungere verticalmente, partendo dal basso, le note espresse dalle lettere, nello stesso modo del sistema tradizionale. La durata delle note verticali avrà la stessa durata della frazione della base, in caso diverso, ovvero, se una o più note dell’accordo abbiano durate diverse, verrà scritto il valore in corrispondenza e parallelamente alla nota.

Per quanto riguarda la parte semantica e quindi tutti le indicazioni che riguardano le tecnica di esecuzione, l’espressione ecc , nulla cambia.

Questo sistema permette, senza alcun limite, la scrittura o la trascrizione di intere partiture orchestrali .

Vantaggi:

• Immediatezza nella lettura/scrittura derivata dalla eliminazione di ogni tipo di chiave o di trasposizione, tutte le note espresse da lettere e numeri saranno sempre note reali.
• Velocità e comodità nella scrittura musicale , ovvero, il non dover ricorrere alla carta da musica.
• Funzione pedagogica  per l’apprendimento della matematica e  della musica, in particolare relazionando empiricamente i suoni a lettere e numeri in età formativa.